《数据分析方法(第二版)》重要概念
重要概念
(一)数据描述性分析
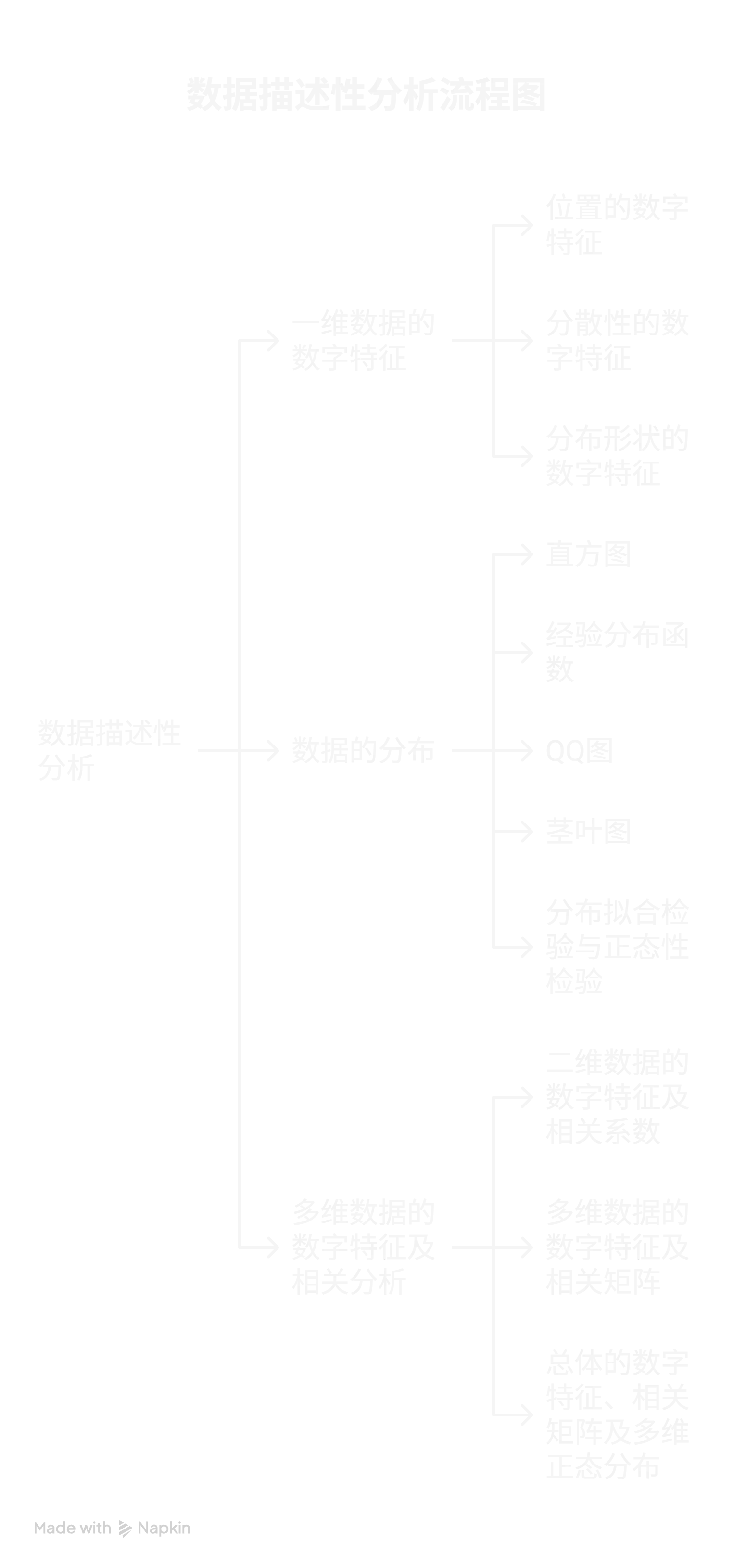
- 一维数据的数字特征
- 表示位置的数字特征:均值、中位数、分位数(如上下四分位数)、三均值。均值易受异常值影响,中位数受异常值影响较小,具有较好的抗扰性或稳健性。分位数是将数据按一定比例分割的数值,三均值是上四分位数、中位数与下四分位数的加权平均。
- 表示分散性的数字特征:方差、标准差、变异系数等。方差是数据相对于均值的偏差平方的平均,标准差是方差的平方根,变异系数是标准差与均值的比值,用于比较不同数据集的离散程度。
- 表示分布形状的数字特征:偏度、峰度等。偏度衡量数据分布的不对称程度,峰度衡量数据分布的尖峰或扁平程度。
- 数据的分布
- 直方图:用矩形的高度表示数据在各个区间的频数或频率,直观展示数据的分布形态。
- 经验分布函数:根据样本数据构建的分布函数,用于估计总体的分布。
- QQ图:用于判断数据是否服从某种特定分布,通过比较样本分位数和理论分位数来评估分布的拟合程度。
- 茎叶图:将数据的整数部分作为茎,小数部分作为叶,展示数据的分布情况,同时保留了原始数据的信息。
- 数据的分布拟合检验与正态性检验:用于检验数据是否符合某种特定的分布,如正态分布。常见的检验方法有卡方检验、Shapiro - Wilk检验等。
- 多维数据的数字特征及相关分析
- 二维数据的数字特征及相关系数:均值向量、协方差、相关系数等。相关系数衡量两个变量之间的线性相关程度,取值范围为[-1, 1]。
- 多维数据的数字特征及相关矩阵:均值向量、方差、协方差矩阵、相关矩阵等。协方差矩阵描述了多个变量之间的协方差关系,相关矩阵则是标准化后的协方差矩阵。
- 总体的数字特征、相关矩阵及多维正态分布:总体的均值向量、协方差矩阵等数字特征,以及多维正态分布的定义和性质。
(二)回归分析
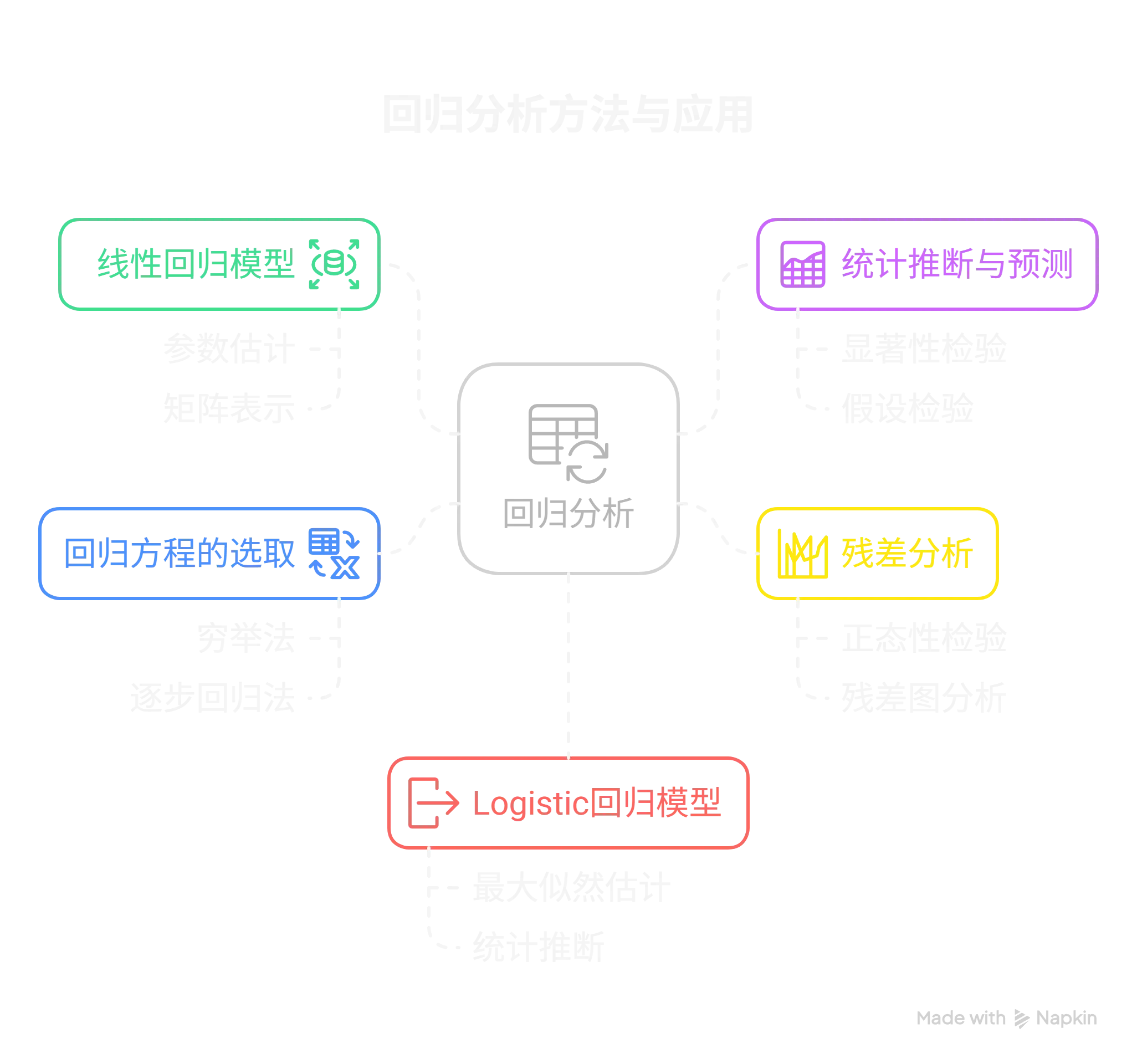
- 线性回归模型及其参数估计
- 线性回归模型及其矩阵表示:用线性方程描述自变量和因变量之间的关系,通过矩阵形式表示可以更方便地进行计算和分析。
- 参数估计及其性质:常用的参数估计方法是最小二乘法,通过最小化误差平方和来估计模型参数。参数估计具有无偏性、有效性等性质。
- 统计推断与预测
- 回归方程的显著性检验:检验回归方程是否显著,即自变量是否对因变量有显著影响。常用的检验方法是F检验。
- 回归系数的统计推断:对回归系数进行假设检验,判断其是否显著不为零。常用的检验方法是t检验。
- 预测及其统计推断:根据回归方程对因变量进行预测,并给出预测的置信区间。
- 与回归系数有关的假设检验的一般方法:可以对回归系数进行各种假设检验,如线性组合的检验等。
- 残差分析
- 误差项的正态性检验:检验误差项是否服从正态分布,常用的检验方法有Shapiro - Wilk检验、正态概率图等。
- 残差图分析:通过绘制残差图来检查模型的假设是否成立,如残差是否具有随机性、是否存在异方差等。
- Box - Cox变换:一种数据变换方法,用于改善数据的正态性和线性关系。
- 回归方程的选取
- 穷举法:对所有可能的自变量组合进行回归分析,选择最优的回归方程。
- 逐步回归法:逐步引入或剔除自变量,直到得到最优的回归方程。
- Logistic回归模型的估计与推断
- Logistic回归模型:用于处理二分类问题,通过Logistic函数将线性组合转换为概率值。
- 参数的最大似然估计与Newton - Raphson迭代解法:使用最大似然估计方法估计模型参数,通过Newton - Raphson迭代算法求解参数。
- Logistic回归模型的统计推断:对Logistic回归模型的参数进行假设检验和置信区间估计。
(三)方差分析
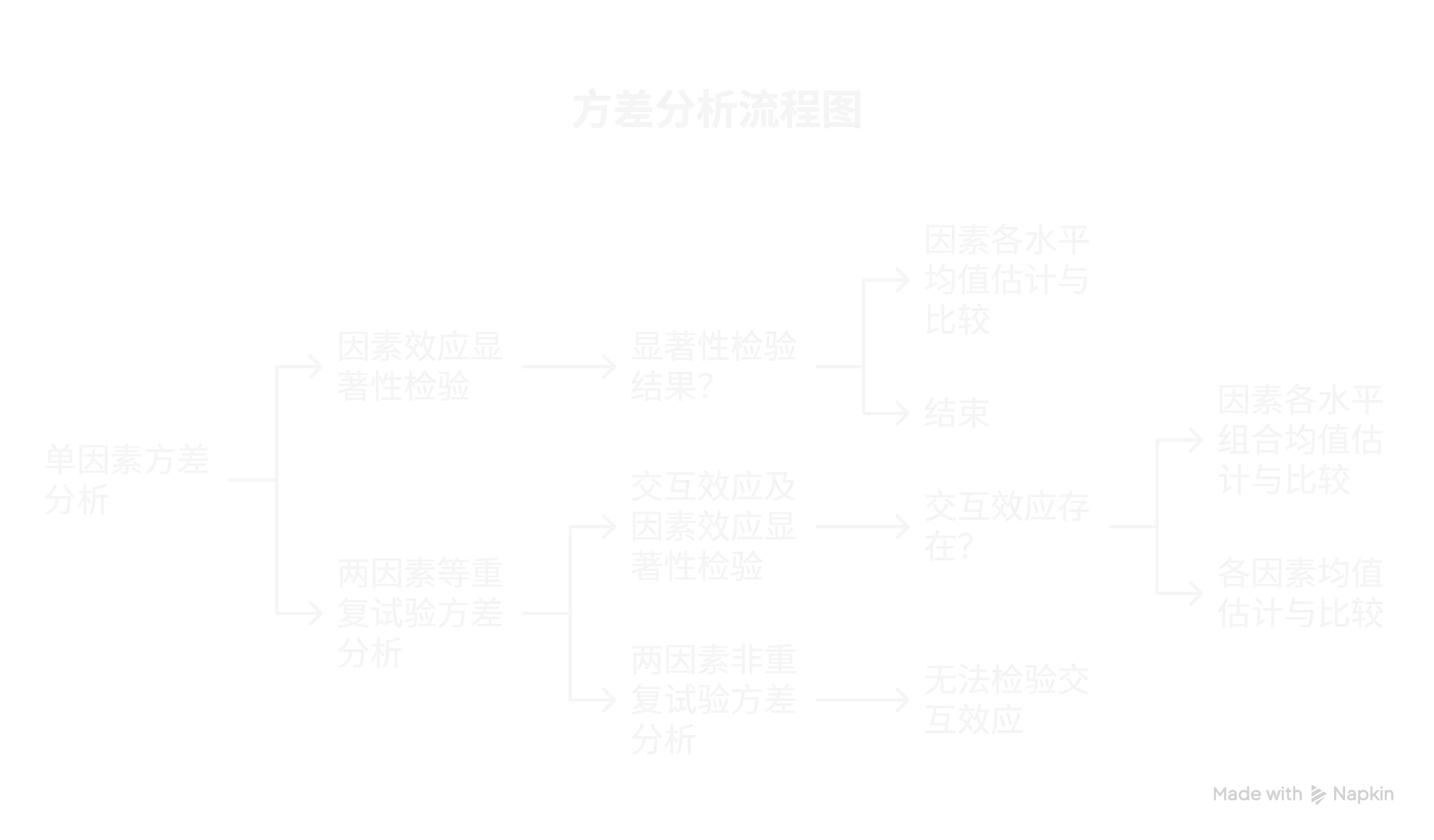
- 单因素方差分析
- 单因素方差分析模型:研究一个因素对因变量的影响,将总变异分解为组间变异和组内变异。
- 因素效应的显著性检验:检验因素的不同水平对因变量是否有显著影响,常用的检验方法是F检验。
- 因素各水平均值的估计与比较:估计因素各水平的均值,并进行均值之间的比较,常用的方法有多重比较方法,如LSD法、Tukey法等。
- 两因素等重复试验下的方差分析
- 统计模型:考虑两个因素对因变量的影响,同时考虑因素之间的交互效应。
- 交互效应及因素效应的显著性检验:检验因素之间的交互效应以及因素的主效应是否显著,常用的检验方法是F检验。
- 无交互效应时各因素均值的估计与比较:在无交互效应的情况下,估计各因素的均值并进行比较。
- 有交互效应时因素各水平组合(Ai, Bj)上的均值估计与比较:在有交互效应的情况下,估计因素各水平组合上的均值并进行比较。
- 两因素非重复试验下的方差分析:在两因素非重复试验的情况下,进行方差分析,由于没有重复观测,无法检验交互效应。
(四)主成分分析与典型相关分析
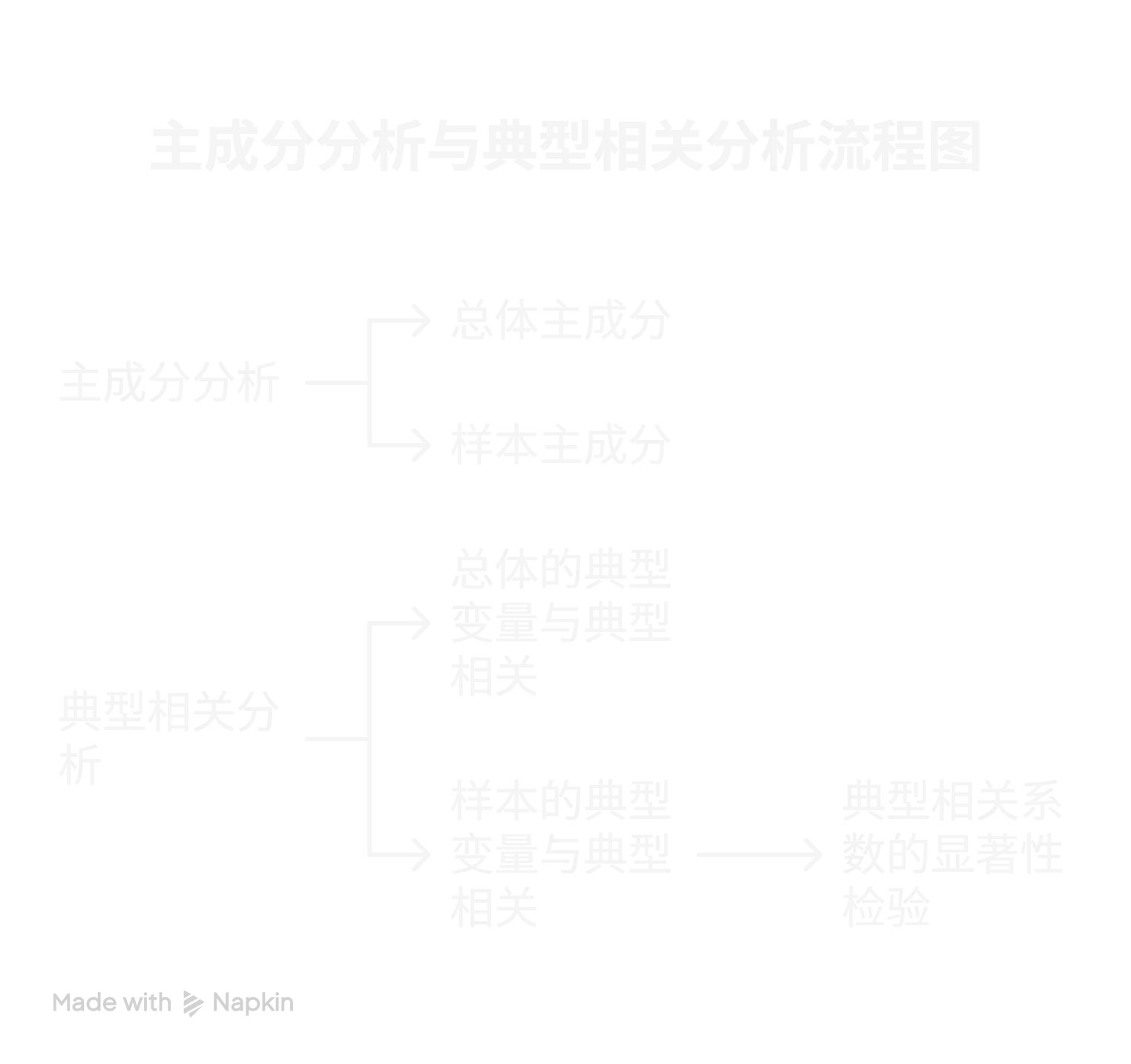
- 主成分分析
- 引言:主成分分析是一种数据降维方法,通过线性变换将原始变量转换为一组互不相关的主成分。
- 总体主成分:总体主成分是总体协方差矩阵的特征向量对应的线性组合,具有最大的方差。
- 样本主成分:根据样本数据计算得到的主成分,用于对样本进行分析和解释。
- 典型相关分析
- 引言:典型相关分析用于研究两组变量之间的相关性,通过寻找两组变量的线性组合,使得它们之间的相关性最大。
- 总体的典型变量与典型相关:总体的典型变量是总体协方差矩阵的特征向量对应的线性组合,典型相关系数衡量两组典型变量之间的相关性。
- 样本的典型变量与典型相关:根据样本数据计算得到的典型变量和典型相关系数。
- 典型相关系数的显著性检验:检验典型相关系数是否显著不为零,常用的检验方法是Bartlett检验。
(五)判别分析
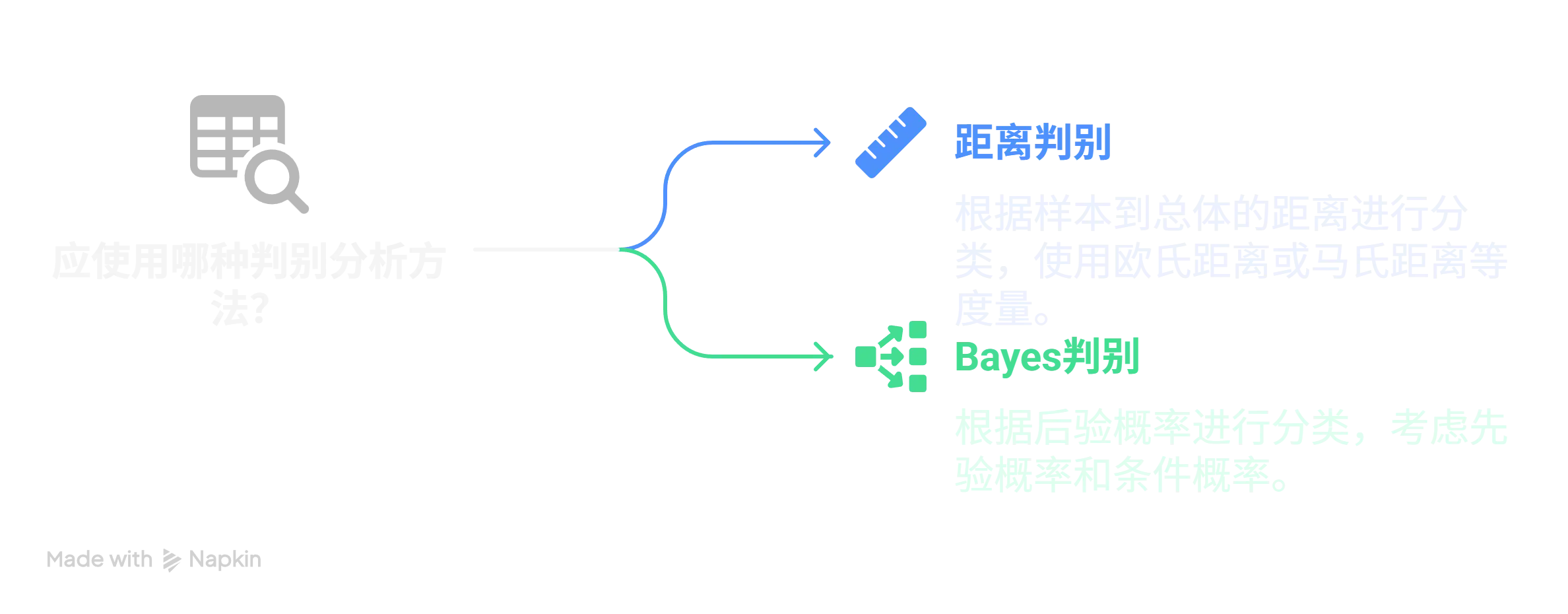
- 距离判别
- 两个总体的距离判别:根据样本到两个总体的距离来判断样本属于哪个总体,常用的距离度量有欧氏距离、马氏距离等。
- 判别准则的评价:评价判别准则的有效性,常用的评价指标有误判率、正确率等。
- 多个总体的距离判别:将距离判别方法推广到多个总体的情况。
- Bayes判别
- Bayes判别的基本思想:根据样本的先验概率和条件概率,计算样本属于各个总体的后验概率,选择后验概率最大的总体作为样本的归属。
- 两个总体的Bayes判别:在两个总体的情况下,应用Bayes判别方法进行分类。
- 多个总体的Bayes判别:将Bayes判别方法推广到多个总体的情况。
(六)聚类分析
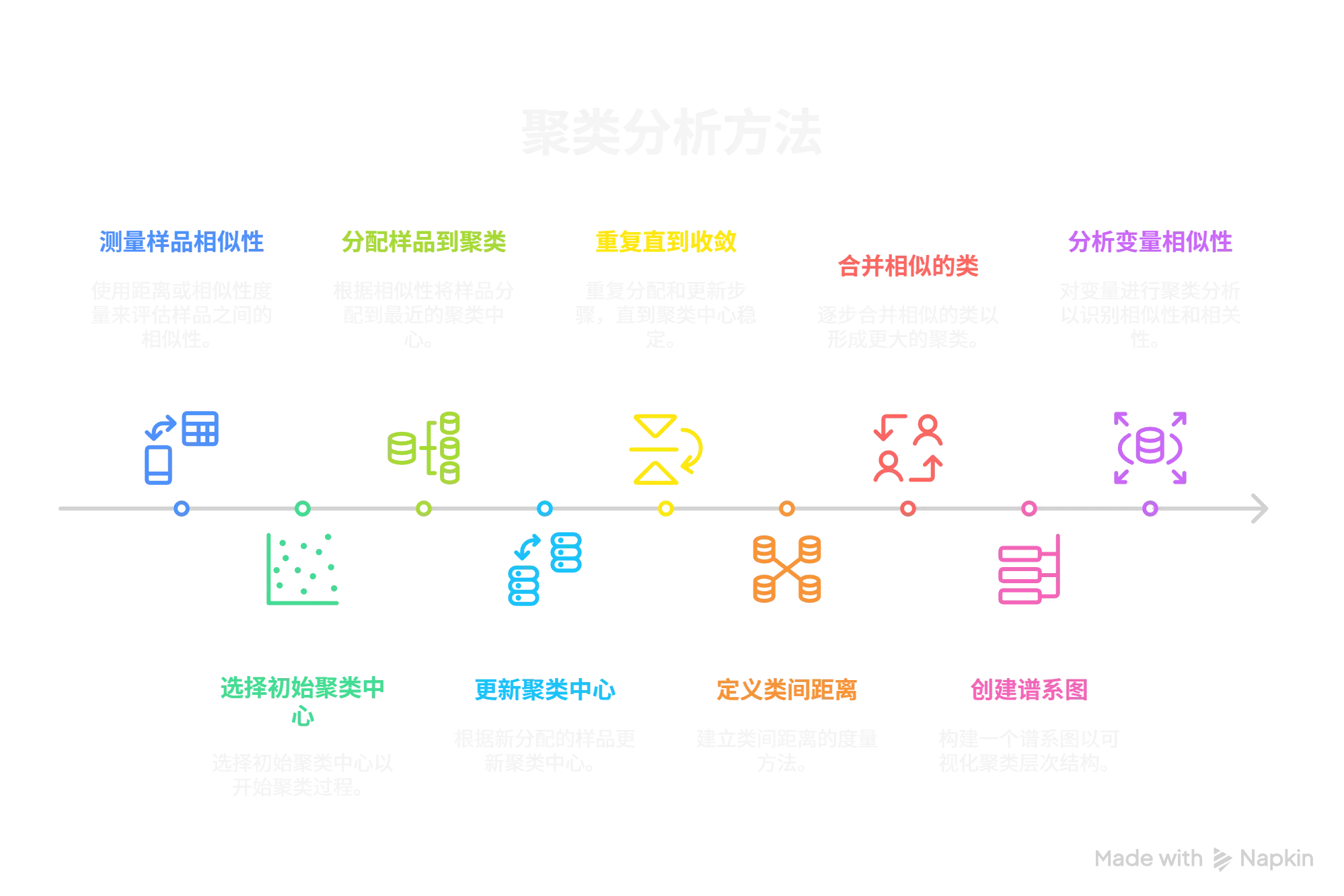
- 样品间相近性的度量:用于衡量样品之间的相似程度,常用的度量方法有距离度量(如欧氏距离、曼哈顿距离等)和相似系数(如相关系数、夹角余弦等)。
- 快速聚类法
- 快速聚类法的步骤:先选择初始聚类中心,然后将样品分配到最近的聚类中心,再更新聚类中心,重复这个过程直到聚类中心不再变化。
- 用Lm距离进行快速聚类:使用Lm距离作为样品间的距离度量进行快速聚类。
- 谱系聚类法
- 类间距离及其递推公式:定义类间距离的度量方法,如最短距离、最长距离、平均距离等,并给出递推公式用于计算类间距离。
- 谱系聚类法的步骤:从每个样品作为一个类开始,逐步合并相似的类,直到所有样品都属于一个类,形成一个谱系图。
- 变量聚类:对变量进行聚类分析,用于发现变量之间的相似性和相关性。
(七)Bayes统计分析
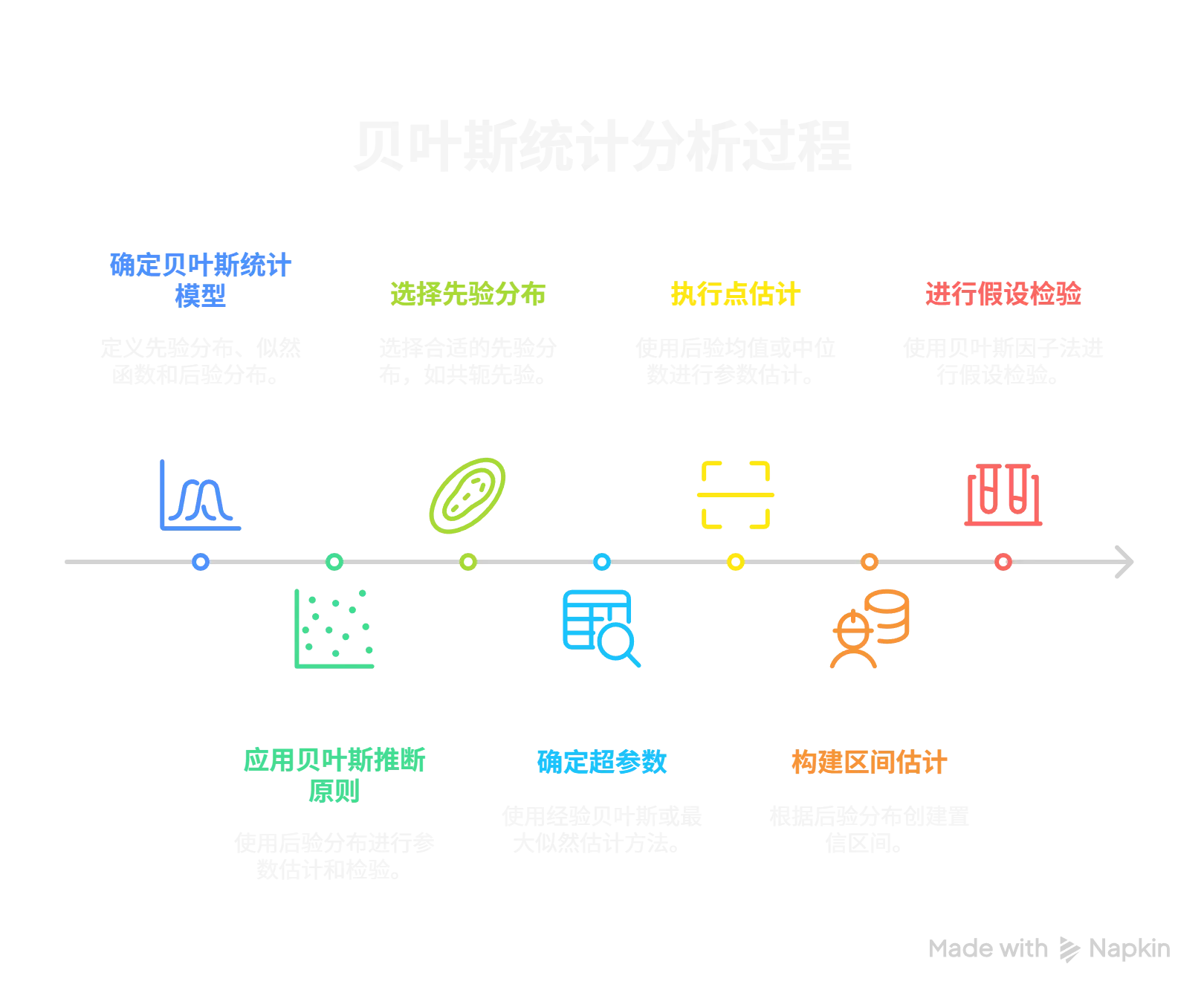
- Bayes统计模型
- Bayes统计分析的基本思想:基于Bayes定理,将先验信息和样本信息结合起来,对参数进行推断。
- Bayes统计模型:定义Bayes统计模型,包括先验分布、似然函数和后验分布。
- Bayes统计推断原则:根据后验分布进行参数的点估计、区间估计和假设检验。
- 先验分布的Bayes假设与不变先验分布:介绍先验分布的Bayes假设和不变先验分布的概念和方法。
- 共轭先验分布:如果先验分布和似然函数的乘积与后验分布属于同一分布族,则称先验分布为共轭先验分布。
- 先验分布中超参数的确定:确定先验分布中的超参数,常用的方法有经验贝叶斯方法、最大似然估计方法等。
- Bayes统计推断
- 参数的Bayes点估计:根据后验分布选择合适的点估计方法,如后验均值、后验中位数等。
- Bayes区间估计:根据后验分布构造参数的置信区间。
- Bayes假设检验:根据后验分布进行假设检验,常用的方法有Bayes因子法等。
此文章版权归XBXyftx所有,如有转载,请註明来自原作者
评论